La fórmula de Erlang B asume una población infinita de orígenes (como usuarios de telefonía), la cual ofrece tráfico en conjunto a N servidores (como líneas en un grupo de troncales). La tasa de llegadas de nuevas llamadas (tasa de nacimiento) es igual a λ y es constante, no depende del número de recursos activos, porque se asume que el total de recursos es infinito. La tasa de abandono (tasa de mortandad) es igual al número de llamadas en progreso dividida por h, la media del tiempo de llamadas en espera. La fórmula calcula la probabilidad de bloqueo en una pérdida del sistema, si un requerimiento no es atendido inmediatamente cuando trata de utilizar un recurso, y este es abortado. Por lo tanto no son encolados. El bloqueo ocurre cuando hay un nuevo requerimiento de recursos, pero todos los servidores ya están ocupados. La fórmula asume que el tráfico que es bloqueado se libera inmediatamente.
A continuación se muestra cómo puede ser expresado recursivamente, en una forma que es usada para calcular tablas de la fórmula de Erlang B:
donde:
- B es la probabilidad de bloqueo
- N es el número de recursos como servidores o circuitos en un grupo
- A = λh es la cantidad de tráfico entrante expresado en Erlangs
La fórmula Erlang B se aplica a los sistemas con pérdidas, tales como sistemas telefónicos tanto fijos como móviles, que no ofrecen almacenamiento de llamadas (es decir, no permiten dejar la llamada "en espera"), y no se pretende que lo hagan. Se asume que las llegadas de llamadas pueden ser modeladas por un proceso de poison, pero es válida para cualquier distribución estadística de tiempos entre llamadas.
Erlang B también es una herramienta para dimensionar tráfico entre centrales de conmutación de voz.
Situacion de bloqueo Funcion Erlang B
Lee mas acerca de esto

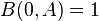
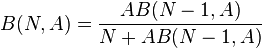




0 comentarios:
Publicar un comentario