Fórmula Engset

Publicado por ANDRES911 en 4:24 | Etiquetas:
La fórmula Engset, así llamada por T. O. Engset, está relacionada pero funciona con una población finita de S orígenes en lugar de la población infinita de orígenes que asume Erlang:

E(N, A, S) = \frac{A^N {\left( \begin{array}{c} S \\ N \end{array} \right)}} {\sum_{i=0}^NA^i {\left( \begin{array}{c} S \\ i \end{array} \right)}}


Esto puede puede ser expresado recursivamente del siguiente modo, en una forma que es usada para calcular las tablas de la fórmula Engset:
E(0, A, S) = 1 \,
E(N, A, S) = { {A(S-N+1)E(N-1,A,S)} \over {N+A(S-N+1)E(N-1,A,S)} } \,


donde:

* E es la probabilidad de bloqueo
* A es el tráfico en Erlangs generado por cada origen cuando está desocupado
* S es el número de orígenes
* N es el número de servidores

De nuevo, se asume que las llamadas que llegan pueden ser modeladas por una distribución Poisson y que los tiempos de espera son descriptos por una distribución exponencial negativa. Sin embargo, debido a que hay un número finito de servidores, la tasa de llegada de las nuevas llamadas decrece a medida que nuevos orígenes (como abonados telefónicos) se vuelven ocupados y por lo tanto no pueden originar nuevas llamadas. Cuando N = S, la fórmula se reduces a una distribución binomial.
viernes, 12 de junio de 2009

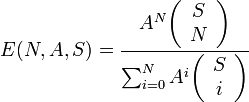
0 comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)